第2章: 音を見る

Last Change:24-May-2016.
Author:qh73xe
contents:sin 波の作成、畳み込み, フーリエ変換

本章の目的は音が波形であることを確かめることです。 そのため、まずは用意した既存の wav データを可視化し、 その特性を観察します。

続いて今度は人工的にサイン波を作成し、 これを wav ファイルにし音を作成してみます。

最後に波形の特徴である周波数について説明をしていきます。

音データの波形

早速音が波形であることを確認してみましょう。 ここでは 前の章で行ったように まずは wav ファイルを読み込み、 そのデータを plot していきます。

C において plot 処理を一から記述するのは少々面倒なので、 ここでは gnu-plot を使用することにします。

$ sudo dnf install gnuplot

gnu_plot を C から操作する

まずは gnu plot を C から操作することを考えます。

test_plot.c
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
#include <stdio.h>

int main(void){
  FILE *gp;

  gp = popen("gnuplot -persist","w");
  fprintf(gp, "plot sin(x)\n");

  pclose(gp);

  return 0;
}

c で外部環境を操作するには、 popen 関数を使用します。 上の例では gp に gnuplot に対する操作手段ができており、 次の行で gnuplot のコマンドを gnuplot のプロセスに渡しています。 最後に pclose で gnuplot のプロセスを殺します。 これがないと、上記のプロセスがゾンビになるので注意してください。

音の大きさを可視化する

それでは早速以下の音の波形データを確認してみましょう。 以下に二つの wav ファイルを置いておきます。 一つがギターの音で、もう一つはリコーダーの音です。

これを読み込み、可視化するには、前回作成した wave.h を利用して 以下のようなコードを記述します。

ex2_0.c
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <stdio.h>
#include <stdlib.h>
#include "wave.h"

int main(void)
{
  /* ---- 変数宣言 ---- */
  MONO_PCM pcm0;
  int n, i;
  double x, y;
  double min, max;
  FILE *gp;

  /* ---- wav の読み込み ---- */
  mono_wave_read(&pcm0, "../guitar_A4.wav");
  printf(
    "HEAD\nfs: %d\nbits: %d\nlength: %d\n",
    pcm0.fs, pcm0.bits, pcm0.length
  );
  /* ---- pcm0.s の最大値と最小値を取得 ---- */
  min = max = pcm0.s[0];
  for (i = 0; i < pcm0.length; i++){
    if (pcm0.s[i] < min) min = pcm0.s[i];
    if (pcm0.s[i] > max) max = pcm0.s[i];
  }

  /* ---- グラフ作成 ---- */
  gp = popen("gnuplot -persist","w");
  fprintf(gp, "set xrange [0:%d]\n", pcm0.length);
  fprintf(gp, "set yrange [%f:%f]\n", min, max);
  fprintf(gp, "plot '-' with lines linetype 1 title \"wave\"\n");
  for (n = 0; n < pcm0.length; n++){
    x = n;
    y = pcm0.s[n];
    fprintf(gp,"%f\t%f\n", x, y);
  }
  fprintf(gp,"e\n");
  pclose(gp);
  free(pcm0.s);
  return 0;
}

このコードは ギターのファイルを前提にしていますので、 リコーダーの音をみるばあいには、ファイル名を変更してください。

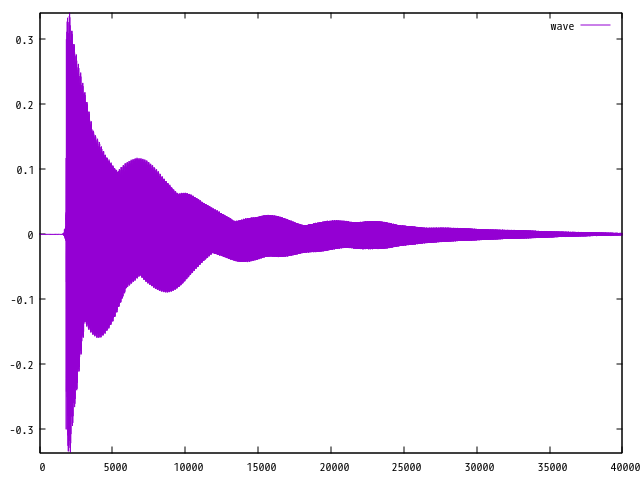
それぞれの音と以下のように可視化されます。

guitar_A4.wav のエンベローブ recorder_A4.wav のエンベローブ
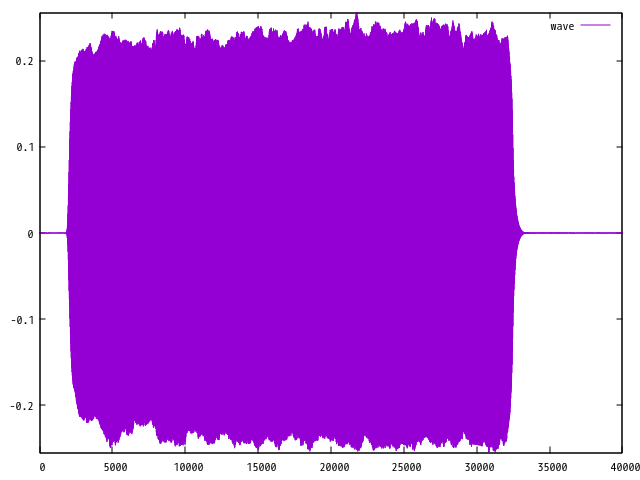fig0_1 fig0_2

音声ファイルは 5 秒間しかありませんが、 標本化周波数は 8kHz であるため、データ数は 40000 個もあります。

そのため、上記のように全てのデータを表示してしまうと、 波形の概形、 エンベローブ のみが、表示されることになります。

エンベローブは振幅の大きさの時間変化を示しています。 これは音の大きさの時間変化であるということもできます。

この特徴は音の発生メカニズムと関係があります。 ご存知の通り、ギターの音は、弦を一回弾いた音です。 それに対し、リコーダーは息を吹いている間、ずっと鳴り続けます。 エンベローブを見ることでこのような発生の違いを見ることができます。

音色を可視化する

では、それぞれの音をもう少し、小さい範囲で見てみましょう。 具体的には 20000 - 20128 までのサンプルを観察します(0からでは音が鳴っていないので)。

以下に可視化用のスクリプトを示します. これは guitar_A4.wav が設定されていますので、 recorder_A4.wav を観察する場合、ファイル名をいじってください。

ex2_0_1.c
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <stdio.h>
#include <stdlib.h>
#include "wave.h"

int main(void)
{
  /* ---- 変数宣言 ---- */
  MONO_PCM pcm0;
  int n, i, str, end;
  double x, y;
  double min, max;
  FILE *gp;
  str = 20000;
  end = str + 128;

  /* ---- wav の読み込み ---- */
  mono_wave_read(&pcm0, "../guitar_A4.wav");
  printf(
    "HEAD\nfs: %d\nbits: %d\nlength: %d\n",
    pcm0.fs, pcm0.bits, pcm0.length
  );
  /* ---- pcm0.s の最大値と最小値を取得 ---- */
  min = max = pcm0.s[str];
  for (i = 0; i < end; i++){
    if (pcm0.s[i] < min) min = pcm0.s[i];
    if (pcm0.s[i] > max) max = pcm0.s[i];
  }

  /* ---- グラフ作成 ---- */
  gp = popen("gnuplot -persist","w");
  fprintf(gp, "set xrange [0:%d]\n", 128);
  fprintf(gp, "set yrange [%f:%f]\n", min, max);
  fprintf(gp, "plot '-' with lines linetype 1 title \"wave: %d-%d\"\n", str, end);
  for (n = str; n < end; n++){
    x = n - str;
    y = pcm0.s[n];
    fprintf(gp,"%f\t%f\n", x, y);
  }
  fprintf(gp,"e\n");
  pclose(gp);
  free(pcm0.s);
  return 0;
}
guitar_A4 recorder_A4
fig1_1 fig1_2

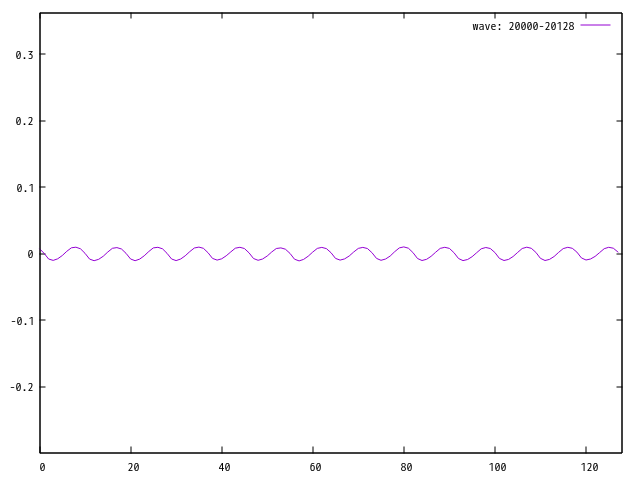
リコーダーと、ギターでは随分形状が異なることが分かると思います。 ギターの波形がギザギザしているのに対し、 リコーダーの波形は、丸みをおびています。

このように音色と波形の形状は関連をしています。

高さを可視化する

づついては、もう一つ wav データを提示します。 これはギターの音ですが、前の例より高い音になっています。

このファイルも 20000 - 20128 までのサンプルを観察してみましょう。

  • コードは読み込みのファイル名を変更するだけなので提示しません。
guitar_A4 guitar_A5
fig1_1 fig1_3

今までの wav ファイルはすべて、周期性のある波形でした。 波形の周期は音の高さに関連していて、 周期が短いと高い音、長いと低い音になります。

  • ここで “関連していて” といっているのは “高さ” という表現が 心理量であるためです。

音の高さは波形の周期の逆数である 基本周波数 によって表現できます。 波形の周期を \(t_0\) , 基本周波数を \(f_0\) とすると、 両者の関係は以下の通りです。

\[f_0 = \frac{1}{t_0}\]

注釈

12 平均律音階

提示したファイル名の A4 とか A5 というのは、 楽器の 12 平均律音階 に基づいて付けられています。

音データの作成

ここまでで、色々な音データの特徴を見て来たので、 今度は人工的に音を作成してみましょう。

詳しい話は次節で行いますが、 音は波形であるため、全て sin 波 で作成することが可能です。

実際に作ってみましょう。 まず、基本周波数 \(f_0\) のサイン波は以下の式で定義できます。

\[s(n) = A \sin{\frac{2\pi f_0 n}{f_s}}\]
  • \(s(n)\) : あるサンプリングポイント \(n\) の時のサイン波
  • \(A\) : 振幅の大きさ(定数)
  • \(f_s\) : 標本化周波数

早速サイン波を C で作成してみましょう。

ex2_1_0.c
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "wave.h"

int main(void)
{
  /* ---- 変数宣言 ---- */
  MONO_PCM pcm1;
  int n;
  double A, f0;

  /* ---- 可視化用 ---- */
  double x, y, min, max;
  int str, end;
  FILE *gp;
  str = 2000;
  end = str + 128;

  /* ---- 定数項 ---- */
  pcm1.fs = 8000;
  pcm1.bits = 16;
  pcm1.length = 8000;
  pcm1.s = calloc(pcm1.length, sizeof(double)); // メモリ確保
  scanf("%lf", &A);
  scanf("%lf", &f0);
  printf("A: %f\n", A);
  printf("f0: %f\n", f0);

  /* ---- サイン波の作成 ---- */
  for (n = 0; n < pcm1.length; n++){
      pcm1.s[n] = A * sin(2.0 * M_PI * f0 * n / pcm1.fs);
  }
  mono_wave_write(&pcm1, "result.wav");

  /* ---- s の最大値と最小値を取得 ---- */
  min = max = pcm1.s[str];
  for (n = 0; n < end; n++){
    if (pcm1.s[n] < min) min = pcm1.s[n];
    if (pcm1.s[n] > max) max = pcm1.s[n];
  }

  /* ---- グラフ作成 ---- */
  gp = popen("gnuplot -persist","w");
  fprintf(gp, "set xrange [0:%d]\n", 128);
  fprintf(gp, "set yrange [%f:%f]\n", min, max);
  fprintf(gp, "plot '-' with lines linetype 1 title \"sin\"\n");
  for (n = str; n < end; n++){
    x = n - str;
    y = pcm1.s[n];
    fprintf(gp,"%f\t%f\n", x, y);
  }
  fprintf(gp,"e\n");
  pclose(gp);
  free(pcm1.s);
  return 0;
}

このスクリプトを実行すると、 二つの入力を要求されます。 最初の入力が A で二つ目の入力が f0 です.

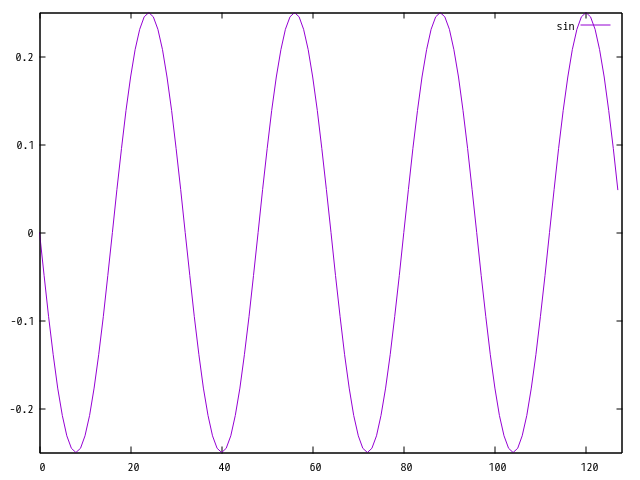
../../../../_images/sin1.png

A: 0.25, f0: 250.0

入力値を変えるたびに図と wav ファイル(result.wav) が作成されるようになっているので、色々遊んでみてください。

警告

gcc に関して

Linux/gcc を使用して上記コードをビルドしようとすると、 そのままでは上手く行かない場合があります。 そのような場合 gcc -lm hoge.c としてください。

重ね合わせ

ある程度, 一つのサイン波で遊ぶことにも慣れてきたら、 今度は上記のサイン波を幾つか混ぜてみましょう。 適当ではありますが、2種類のサイン波を重ね合わせたサイン波を音声にした例を以下に 置いておきます。

ex2_1_1.c
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "wave.h"

int main(void)
{
  /* ---- 変数宣言 ---- */
  MONO_PCM pcm1, pcm2, pcm3;
  int n;
  double A, f0;

  /* ---- 可視化用 ---- */
  double x, y, min, max;
  int str, end;
  FILE *gp;
  str = 2000;
  end = str + 128;

  /* ---- 定数項 ---- */
  pcm1.fs = 8000;
  pcm1.bits = 16;
  pcm1.length = 8000;
  pcm1.s = calloc(pcm1.length, sizeof(double)); // メモリ確保

  pcm2.fs = 8000;
  pcm2.bits = 16;
  pcm2.length = 8000;
  pcm2.s = calloc(pcm2.length, sizeof(double)); // メモリ確保

  pcm3.fs = 8000;
  pcm3.bits = 16;
  pcm3.length = 8000;
  pcm3.s = calloc(pcm2.length, sizeof(double)); // メモリ確保

  /* ---- サイン波の作成 ---- */
  A = 0.25;
  for (n = 0; n < pcm1.length; n++){
      pcm1.s[n] = A * sin(2.0 * M_PI * 250.0 * n / pcm1.fs);
  }

  for (n = 0; n < pcm2.length; n++){
      pcm2.s[n] = A * sin(2.0 * M_PI * 500.0 * n / pcm2.fs);
  }

  /* ---- 畳み込み ---- */
  for (n = 0; n < pcm3.length; n++){
      pcm3.s[n] = pcm1.s[n] + pcm2.s[n];
  }

  mono_wave_write(&pcm3, "result.wav");

  /* ---- s の最大値と最小値を取得 ---- */

  min = max = pcm1.s[str];
  for (n = 0; n < end; n++){
    if (pcm1.s[n] < min) min = pcm1.s[n];
    if (pcm1.s[n] > max) max = pcm1.s[n];
  }
  for (n = 0; n < end; n++){
    if (pcm2.s[n] < min) min = pcm2.s[n];
    if (pcm2.s[n] > max) max = pcm2.s[n];
  }
  for (n = 0; n < end; n++){
    if (pcm3.s[n] < min) min = pcm3.s[n];
    if (pcm3.s[n] > max) max = pcm3.s[n];
  }



  /* ---- グラフ作成 ---- */
  gp = popen("gnuplot -persist","w");
  fprintf(gp, "set multiplot\n");
  fprintf(gp, "set xrange [0:%d]\n", 128);
  fprintf(gp, "set yrange [%f:%f]\n", min, max);

  fprintf(gp, "plot '-' with lines lt 2 lc rgb \"red\" lw 1\n");
  for (n = str; n < end; n++){
    x = n - str;
    y = pcm1.s[n];
    fprintf(gp,"%f\t%f\n", x, y);
  }
  fprintf(gp, "e\n");

  fprintf(gp, "plot '-' with lines lt 2 lc rgb \"salmon\" lw 1\n");
  for (n = str; n < end; n++){
    x = n - str;
    y = pcm2.s[n];
    fprintf(gp,"%f\t%f\n", x, y);
  }
  fprintf(gp,"e\n");

  fprintf(gp, "plot '-' with lines lt 2 lc rgb \"green\" lw 10\n");
  for (n = str; n < end; n++){
    x = n - str;
    y = pcm3.s[n];
    fprintf(gp,"%f\t%f\n", x, y);
  }
  fprintf(gp,"e\n");
  fprintf(gp, "set nomultiplot\n");
  fprintf(gp, "exit\n");
  fflush(gp);
  pclose(gp);

  free(pcm1.s);
  free(pcm2.s);
  return 0;
}

ここで 重ね合わせ という数学用語が出てきますが、 現状ではとりあえず普通の足し算であると考えくれてよいです。

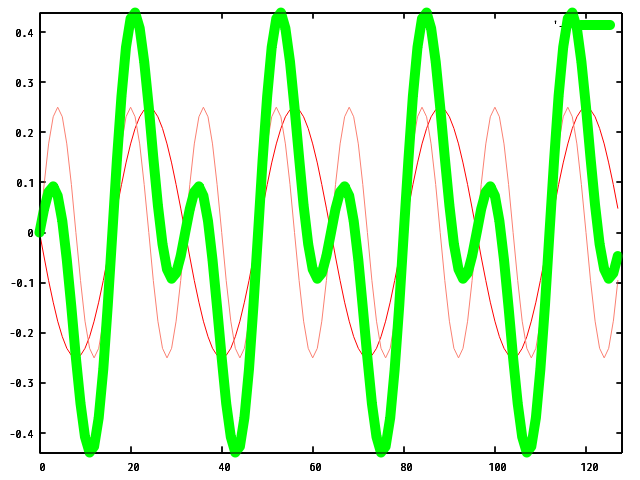
../../../../_images/sin2.png

この時一番小さな周波数が 基本周波数 となり、 これによって音の高さが変わります。

なお、基本周波数のサイン波を 基本音 , その整数倍の周波数のサイン波を 倍音 と呼びます。

ここで、全ての周期的な波形は、周波数が整数倍の関係にあるサイン波を重ね合わせることで合成することができると知られています。

  • このページでは数学の話をする気は基本的にないのですが、 詳しい説明は フーリエ級数展開とかでググるとよいと思います。

具体的にどのように音を再現するのかは一旦置いておき、 まずはいくつかの周期関数を実際にサイン波で作成してみようと思います。

最初に作成してみるのは以下の数式によって作成される周期関数です。

\[\begin{split}s(n) &= \sum_{i=0}^{\infty} \frac{A}{i} \sin(\frac{2 \pi i f_0 n}{f_s}) \\ &= A \sin(\frac{2 \pi f_0 n}{f_s}) + \frac{A}{2} \sin(\frac{2 \pi 2 f_0 n}{f_s}) + \frac{A}{3} \sin(\frac{2 \pi 3 f_0 n}{f_s}) + \cdots + \frac{A}{i} \sin(\frac{2 \pi i f_0 n}{f_s})\end{split}\]

数学上は \(\infty\) までの総和を取りたいのですが、 PC 上では難しいので、上限を 2, 3, 15 までとった値を示すことにします。

実装としては以下のコードを記述すればよいでしょう。

ex2_2.c
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "wave.h"

/* ---- のこぎり波作成関数 ---- */
MONO_PCM mk_saw_tooth(int i_max){
  MONO_PCM pcm;
  int n, i;
  double A, f0;

  pcm.fs = 8000;
  pcm.bits = 16;
  pcm.length = 8000;
  pcm.s = calloc(pcm.length, sizeof(double));
  A = 0.25;
  f0 = 250.0;
  for (n = 0; n < pcm.length; n++)
  {
    for (i = 1; i <= i_max; i++)
    {
      pcm.s[n] += A / i * sin(2.0 * M_PI * f0 * i * n / pcm.fs);
    }
  }
  return pcm;
}

/* ---- グラフ作成関数 ---- */
int mkplot(MONO_PCM pcm){
  double x, y, min, max;
  FILE *gp;
  int str, end, n;

  str = 2000;
  end = str + 128;

  min = max = pcm.s[str];
  for (n = 0; n < end; n++){
    if (pcm.s[n] < min) min = pcm.s[n];
    if (pcm.s[n] > max) max = pcm.s[n];
  }

  gp = popen("gnuplot -persist","w");
  fprintf(gp, "set xrange [0:%d]\n", 128);
  fprintf(gp, "set yrange [%f:%f]\n", min, max);
  fprintf(gp, "plot '-' with lines lt 2 lc rgb \"green\" lw 10\n");
  for (n = str; n < end; n++){
    x = n - str;
    y = pcm.s[n];
    fprintf(gp,"%f\t%f\n", x, y);
  }
  fprintf(gp,"e\n");
  fprintf(gp, "exit\n");
  fflush(gp);
  pclose(gp);
  return 0;
}

int main(void)
{
  MONO_PCM pcm2, pcm3, pcm15;
  pcm2 = mk_saw_tooth(2);
  pcm3 = mk_saw_tooth(3);
  pcm15 = mk_saw_tooth(15);
  mkplot(pcm2);
  mkplot(pcm3);
  mkplot(pcm15);

  mono_wave_write(&pcm2, "result.wav");
  mono_wave_write(&pcm15, "result1.wav");
  free(pcm2.s);
  free(pcm3.s);
  free(pcm15.s);
  return 0;
}

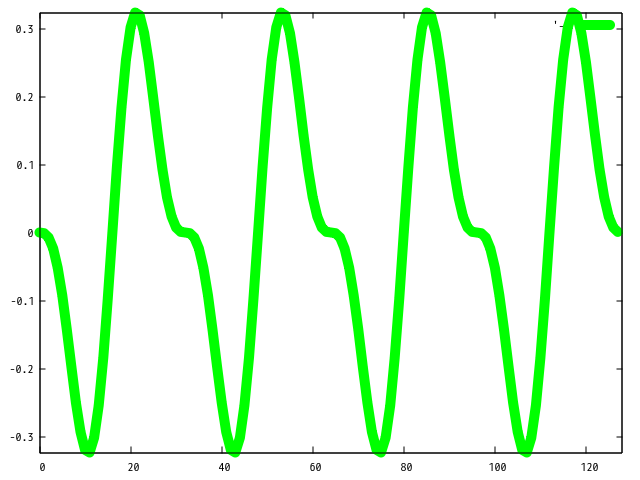
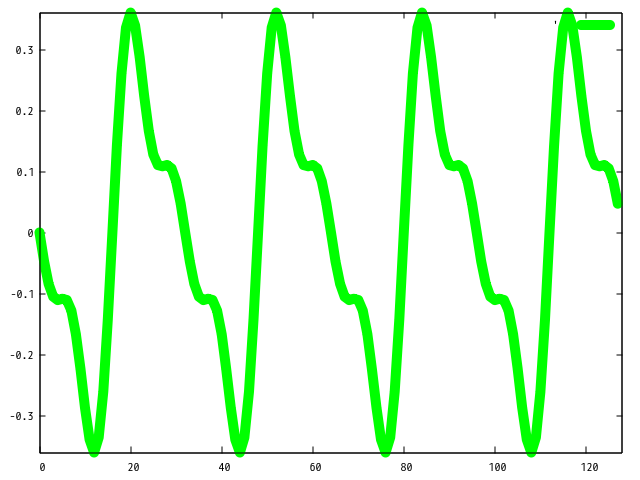
上記コードを実行すると以下のプロットが取得できます。

i=2 i=3 i=15
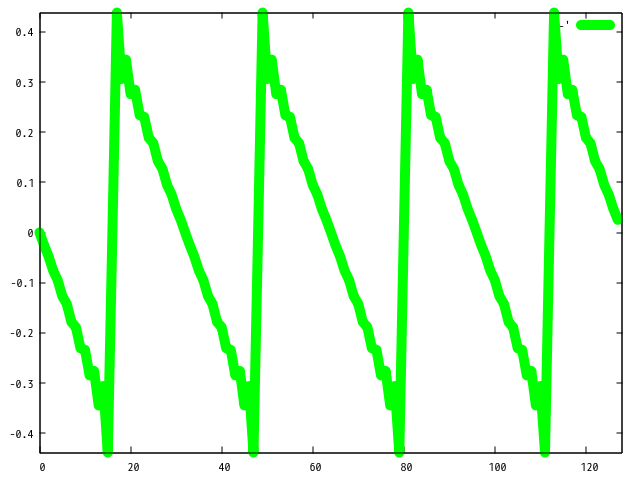fig2_1 fig2_2 fig2_3

i を増やせば増やす程にギザギザ な波形になることが分かるかと思います。 このような波形をのこぎり波といいます。

また \(i=2, i=15\) の場合の音声を wav ファイルに出力するようにしているのので、 これを再生することで、この波形がどのような音であるのがが分かると思います。

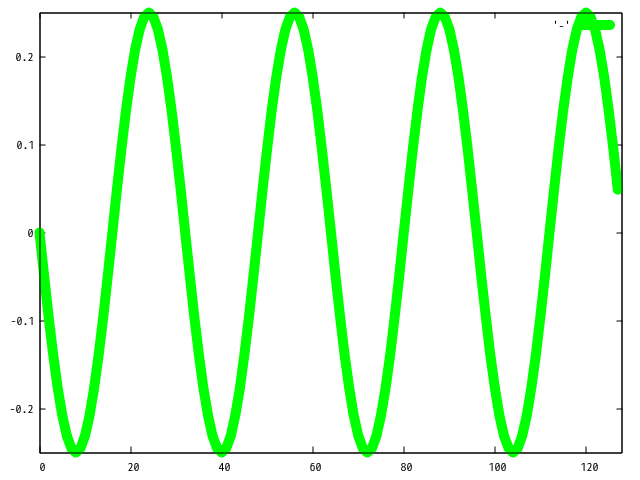
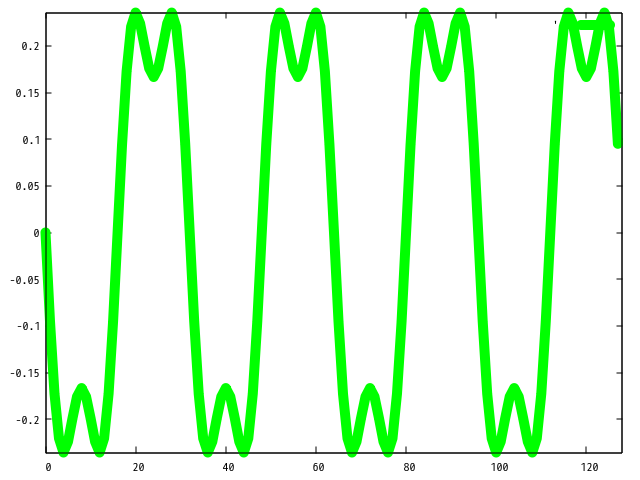
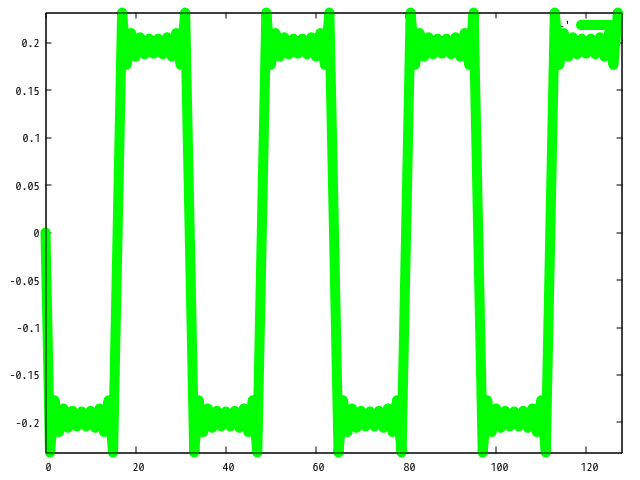
もう一つ周期関数を考えてみましょう。 今度は先程ののこぎり波の、 i が奇数の時のみを重ね合わせます。 つまり数式的には以下のような感じです。

\[\begin{split}s(n) &= sum_{i=0}^{\infty} \frac{A}{2 i - 1} \sin(\frac{2 \pi 2i - 1 f_0 n}{f_s}) &= A \sin(\frac{2 \pi f_0 n}{f_s}) + \frac{A}{3} \sin(\frac{2 \pi 3 f_0 n}{f_s}) + \frac{A}{5} \sin(\frac{2 \pi 5 f_0 n}{f_s}) + \cdots + \frac{A}{i} \sin(\frac{2 \pi i f_0 n}{f_s})\end{split}\]

実装に関して詳しい説明はいらないと思います。 重ね合わせの部分に関して i が奇数の時のみ足すというルールが加わっているだけです。

ex2_3.c
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "wave.h"

/* ---- のこぎり波作成関数 ---- */
MONO_PCM mk_saw_tooth(int i_max){
  MONO_PCM pcm;
  int n, i;
  double A, f0;

  pcm.fs = 8000;
  pcm.bits = 16;
  pcm.length = 8000;
  pcm.s = calloc(pcm.length, sizeof(double));
  A = 0.25;
  f0 = 250.0;
  for (n = 0; n < pcm.length; n++)
  {
    for (i = 1; i <= i_max; i++)
    {
      pcm.s[n] += A / i * sin(2.0 * M_PI * f0 * i * n / pcm.fs);
    }
  }
  return pcm;
}

/* ---- グラフ作成関数 ---- */
int mkplot(MONO_PCM pcm){
  double x, y, min, max;
  FILE *gp;
  int str, end, n;

  str = 2000;
  end = str + 128;

  min = max = pcm.s[str];
  for (n = 0; n < end; n++){
    if (pcm.s[n] < min) min = pcm.s[n];
    if (pcm.s[n] > max) max = pcm.s[n];
  }

  gp = popen("gnuplot -persist","w");
  fprintf(gp, "set xrange [0:%d]\n", 128);
  fprintf(gp, "set yrange [%f:%f]\n", min, max);
  fprintf(gp, "plot '-' with lines lt 2 lc rgb \"green\" lw 10\n");
  for (n = str; n < end; n++){
    x = n - str;
    y = pcm.s[n];
    fprintf(gp,"%f\t%f\n", x, y);
  }
  fprintf(gp,"e\n");
  fprintf(gp, "exit\n");
  fflush(gp);
  pclose(gp);
  return 0;
}

int main(void)
{
  MONO_PCM pcm2, pcm3, pcm15;
  pcm2 = mk_saw_tooth(2);
  pcm3 = mk_saw_tooth(3);
  pcm15 = mk_saw_tooth(15);
  mkplot(pcm2);
  mkplot(pcm3);
  mkplot(pcm15);

  mono_wave_write(&pcm2, "result.wav");
  mono_wave_write(&pcm15, "result1.wav");
  free(pcm2.s);
  free(pcm3.s);
  free(pcm15.s);
  return 0;
}

コードを実行すると以下のプロットを得ます。 どうでしょうか？ 予想していた形と同じもの、でました？ このような波形を矩形波といいます。

i=2 i=3 i=15
fig3_1 fig3_2 fig3_3

まとめ

ここまでで、サイン波、のこぎり波、矩形波と、 三種類の波形を人工的に作成し、音に変換してみました。

勿論、ここで紹介している波形は現実世界の音に較べて単純きわまりないものです。 しかし、とりあえず、以下の事実に関してはある程度了解いただけたと思います。

  • 音は波形である。
  • 音の波形はサイン波が元になっている
  • 二つ以上のサイン波を重ね合わせたい場合、基本足し算をすればよい

上記の話を念頭におくと、 現実の音に関してもサイン波で表現することができそうかなと思われるかと思います。 そしてこの際に重要なのは、結局どのようなサイン波を重ね合わせたらよいのかという問題になるとご理解頂けると思います。

次節では、上記の問題を解析するための手法として フーリエ変換 というものを紹介して行きます。

高速フーリエ変換

注釈

コラム2 PSG音源